Diffusion

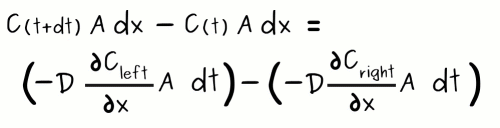
Fick's second law - part II

"You've got to be very careful if you don't know where you're going, because you might not get there."

Yogi Berra

The wonderful thing about the two equations we saw in the previous page is that both are telling us the same thing (they are equal to each other). Therefore, we can say that

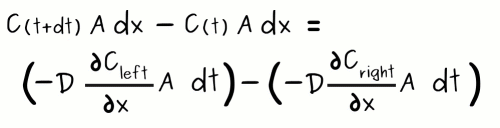
(-D dCleft/dx) A dt - (-D dCright/dx) A dt = C(x,t+dt) A dx - C(x,t) A dx

First, to rearrange this equation, let's first group things together as follows:

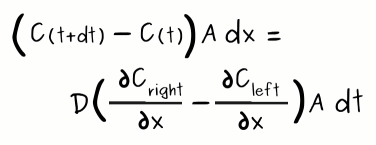
((-D dCleft/dx) - (-D dCright/dx)) A dt = (C(x,t+dt) - C(x,t)) A dx

Then, let's cancel A and switch dt and dx, which yields:

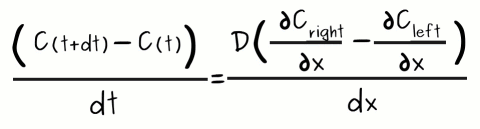
(((-D dCleft/dx) - (-D dCright/dx)))/dx = (C(x,t+dt) - C(x,t))/dt

Finally, let's establish that dx and dt are very small (mathematically let's them tend to zero) and voila!, we have the following:

Isn't this fantastic? In any case, what is important is that we obtained Adolf Fick's famous second law.

Understanding where this expression comes from is an important step in embracing a deep comprehension of this equation.

Here's something to help you remember :

First law, first derivative.
Second law, second derivative.

Thanks John for your comments...

...back to part I

...back to the first law