
Fick's second law
Before we talked about how mosquitoes will "diffuse" from the forest toward the beach. As you may be thinking now, mosquitoes don't really move randomly, because they can fly wherever they want. It's true, and you are right!!!. However, what is important here is to grab the idea that there is a tendency to move from high concentration to low concentration. Now the question is, how long does diffusion take to occur? The answer to this question will require an exploration of Fick's second law.
Let's begin by saying that the Adolf Fick's second law states that :

Great!, but what does that means? In plain words, this equation established that changes in concentration per each unit of time in a region of space is equal to the Diffusion Coefficient (D) times the concentration profile in that region. The second term of the equation is very interesting because it establishes the first derivative of the concentration in time, the speed, is proportional to the second derivative of the concentration in space, or the difference in the gradients. Amusing in a way, isn't it?.
Let's understand why the "speed" of diffusion depends on "the difference of the differences" or, more formally, the second derivative of the concentration. Suppose we have diffusing particles in a long square pipe and we are going to look at the diffusion only in one dimension, let's say x (the length of the pipe). In other words, we care about the particles moving from right to left or left to right, but not up and down or back and forth. Let's now divide our pipe into little squares and give each square a length of dx. Then, from Fick's first law we know that:

This means that, along x, each face of the square will have a certain net flux of particles. Particularly, on the left face, the net amount of particles flowing into our section of interest (J) will be:
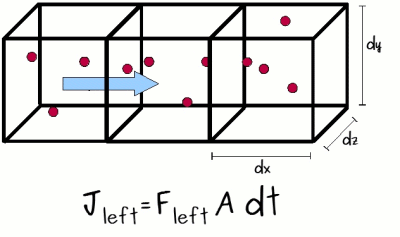
In simpler terms, the amount of particles (the flux) per area per unit of time (F), times the area available for particles to cross (A, which is dy times dz), times the interval of time of our observation (dt). Replacing F in the previous equation yields:
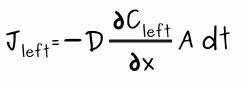
Analogically, for the right face of our square of interest, we obtain for the right side the following:
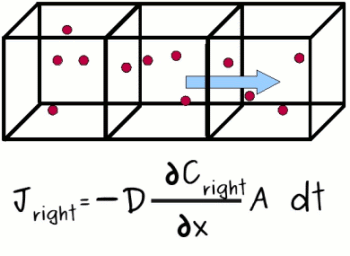
Mathematically, the flux is going from left to right, so if we want to know how many particles we get in the section we are interested in, we can say that the total amount staying in the section we care about is how many we get from the left minus how many we lose on the right. In equation form we have :
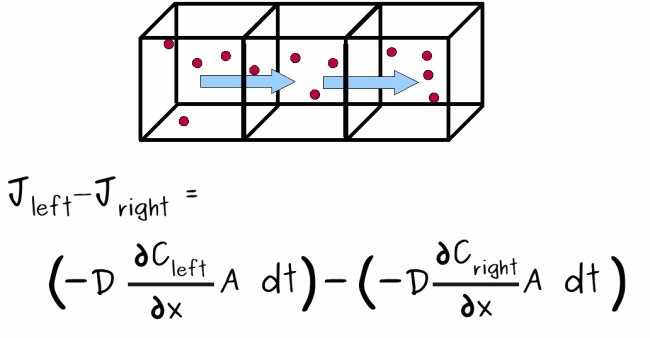
Now that we know what is going on in terms of the space, what is happening in time? Well, we know that the concentration of particles in x at time t is C(x,t), and an instant of time later the concentration is C(x,t+dt). Also, we know that concentration is the amount of particles per unit of volume. Therefore, if we want to know the amount of particles we have, we simply multiply the concentration by the volume we are considering. In our case, the volume will be the area "A" times the length of our section "dx". Then the change in the amount of particles observed in an interval of time equal to dt is :
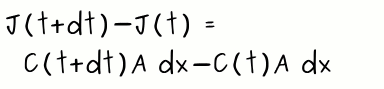
Isn't this great?! Now we have a mathematical representation of our problem. This last equation tell us what happens with the particles in time, while the previous one tells us about what happens spatially. So, how are both equations related? The answer on the next page...