Fick's first law
The most intuitive fact that rules diffusive processes is that freely moving matter tends to go from higher to lower concentration. In reality, moving particles in the absence of any external force wander in space in any direction. Moving back and forth, left to right, up and down, they go everywhere. If there was any sort of gradient or accumulation of these particles in any region, this random dance will result in the homogenization of the concentration of particles throughout all accessible space. This simple vision is the core of Fick's first law.
"Nobody goes there anymore, it's too crowded!" Yogi Berra
Adolf Fick's first law established that the rate of transfer of matter in space is proportional to local differences in the concentration of particles, or, as it is commonly known, concentration gradients. This means that in order to have a net movement, a gradient of particles must exist. However, the First law is referring to a population of particles rather than to each of them individually. In other words, every single diffusing particle will move around within the space which contains it, independently of how many other particles of its species are there.
This requires us to understand more intimately Fick's first law, which mathematically is

where F is the flux of a particle through a single unit of area. D is the diffusion coefficient and C is the concentration of particles. Let me explain this in more detail. Suppose we are looking at a pipe. Then, let's divide the pipe into identical parts. Now, the amount of matter crossing from one section of the pipe to the other is proportional to the difference in concentration between them. In terms of the individual particles, the probability of a particle's crossing will be independent of which section it is contained in. Let's assume that the concentration of particles in the left part of the pipe is higher than in the right part of the pipe. Following this idea, the chance of getting a particle to cross from left to right will be greater than the chance of having a particle come from the right section of the pipe and enter the left one. This idea is represented in the expression with the term
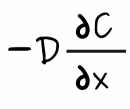
As you can see, the negative sign is there because if the concentration decreases from left to right, the net flux will go from right to left. And, as you may know already, if the concentration decreases from right to left, the net flux will go from left to right. In other words, the gradient and the flux point in opposite directions.
If the reason for the negative sign is not clear yet, I will extend this explanation a little further on the next page...